Easy | Leetcode 347. Top K Frequent Elements

Question

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

---

Solution

Solution 1: Sorting

解題概念：

1. 用一個hashmap把每個元素跟他出現過的次數記錄起來。
2. 由於Map無法排序，我們把Map轉為list，每個list的元素為一個陣列 [數字, 次數]。
3. 對list的第二個元素（出現次數）做排序，由大到小。
4. 最後拿出list中前K個元素的數字做為結果return。
   
   

程式碼：

public class Solution1 {
    public int[] topKFrequent(int[] nums, int k) {
        // 建立一個Hashmap
        Map<Integer, Integer> map = new HashMap<>();

        // 儲存數字與對應出現次數
        for (int num: nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        // 將Map轉為List，List每個元素為一個陣列（數字，出現次數）
        List<int[]> list = new ArrayList<>();

        // 遍歷Map中所有元素，並取出key, value
        for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
            int[] arr = new int[2];
            arr[0] = entry.getKey();
            arr[1] = entry.getValue();
            list.add(arr);
        }

        // 對list的出現次數做排序，降序
        list.sort((a, b) -> Integer.compare(b[1], a[1]));

        // 將前K個元素取出其數字
        int[] result = new int[k];

        for (int i = 0; i < k; i++) {
            result[i] = list.get(i)[0];
        }

        return result;
    }
}

複雜度分析：

• Time complexity: $O(n logn)$
  • 遍歷num所有元素存入map：$O(n)$
  • 將map轉為list：$O(m)$，m為map的key個數，最壞為 $O(n)$
  • 排序：$O(m logm)$，最壞為 $O(n logn)$
  • 取出前K個元素：$O(k)$ => 總共：$O(n logn)$
• Space complexity: $O(n)$
  • 儲存map：$O(m)$，最壞 $O(n)$
  • 儲存list：$O(m)$，最壞 $O(n)$
  • 儲存結果：$O(k)$ => 總共：$O(n)$

Solution2: Min heap

解題概念：

1. 用一個hashmap把每個元素跟他出現過的次數記錄起來。
2. 把Map轉為Heap，每個heap的元素為一個陣列 [數字, 次數]。（建立heap的時候記得設定其排序：by 出現次數）
3. 維持heap大小為K，若超過，把最小的移除，可以保證heap裡面存的是前K大的元素（大小是針對出現次數）
4. 將heap中所有元素一一拿出來，並取出其數字。
   
   

程式碼：

public class Solution2 {
    public int[] topKFrequent(int[] nums, int k) {
        // 建立一個Hashmap
        Map<Integer, Integer> map = new HashMap<>();

        // 儲存數字與對應出現次數
        for (int num: nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        // 建立一個heap，每個元素為一個陣列，指定以陣列第二個元素做排序（出現次數）
        PriorityQueue<int[]> min_heap = new PriorityQueue<>((a, b) -> Integer.compare(a[1], b[1]));

        // 將Map中每組資料加入heap
        for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
            min_heap.offer(new int[]{entry.getKey(), entry.getValue()});
            // heap維持前K大的元素
            if (min_heap.size() > k) {
                min_heap.poll();
            }
        }

        // 將heap中前K個元素取出其數字
        int[] result = new int[k];
        for (int i = 0; i < k; i++) {
            result[i] = min_heap.poll()[0];
        }

        return result;
    }
}

複雜度分析：

• Time complexity: $O(n logk)$
  • 遍歷num所有元素存入map：$O(n)$
  • 將map中元素加入heap（heap大小為k）：每次為 $O(log k)$，總共最多n次：$O(n logk)$。
  • 從heap中取出元素：每次為 $O(log k)$，總共k次：$O(k logk)$。
• Space complexity: $O(n + k)$
  • Hashmap：$O(n)$
  • Heap：最多k個元素，每個元素長度為2陣列：$O(k)$；結果陣列：$O(k)$。
    
    

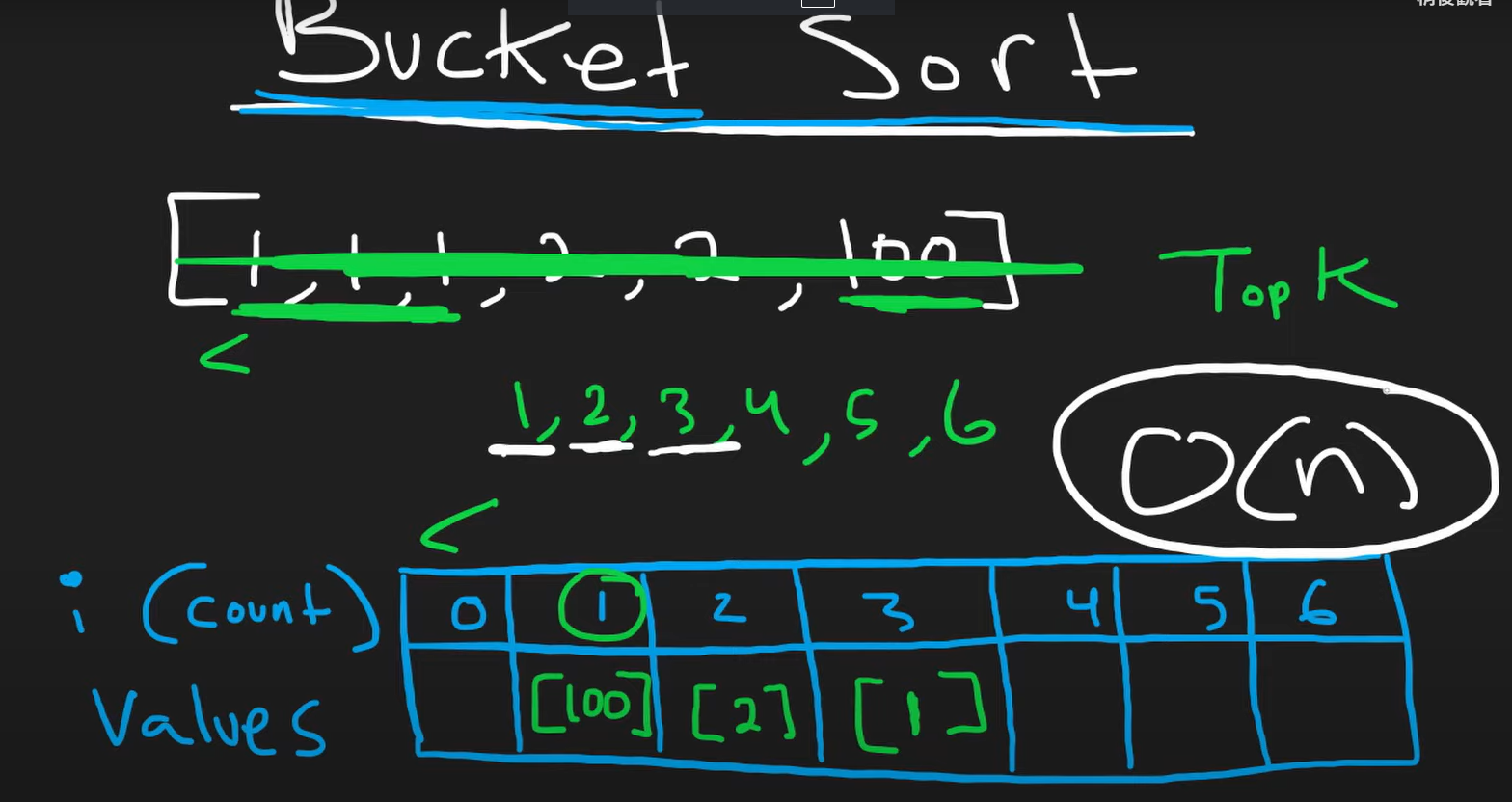
Solution3: Bucket Sort

解題概念：

1. 用一個hashmap把每個元素跟他出現過的次數記錄起來。
2. 建立一個frequncy array，index是出現次數，value是對應到這個出現次數的數字（為一個List）
   • array長度為num個數+1，因為若所有數字都是同一個，最大的count即為num個數。
3. 遍歷這個frequncy array，從index (count)最大開始，若其value list有數字，將他加入reuslt陣列。
   • result陣列個數為k的時候，返回結果。

程式碼：

public class Solution3 {
    public int[] topKFrequent(int[] nums, int k) {
        // 建立一個Hashmap
        Map<Integer, Integer> map = new HashMap<>();

        // 儲存數字與對應出現次數
        for (int num: nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        // 建立freq array，共有num個數+1個元素
        List<Integer>[] freq = new List[nums.length + 1];
        for (int i = 0; i < freq.length; i ++) {
            freq[i] = new ArrayList<>(); // 初始化：值為空list
        }

        // 將map結果依序加入freq陣列中
        // index=出現次數；value=出現該次數的數字list
        for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
            freq[entry.getValue()].add(entry.getKey()); // 將數字加入list中
        }

        int[] result = new int[k];
        int index = 0;
        // 從出現次數最大開始，若他對應到的數字list有值，加入result陣列
        for (int i = freq.length - 1; i >= 0; i--) {
            for (int num: freq[i]) {
                result[index] = num;
                index++;
            }
            // 直到陣列元素=k
            if (index == k) {
                return result;
            }
        }
        return result;
    }
}

複雜度分析：

• Time complexity: $O(n)$
  • 建立map：$O(n)$
  • 建立bucket：$O(n)$
  • 遍歷bucket：$O(n)$
• Space complexity: $O(n)$
  • HashMap大小：$O(n)$
  • 桶空間最多 n+1：$O(n)$
  • 結果陣列大小為 k：$O(k)$