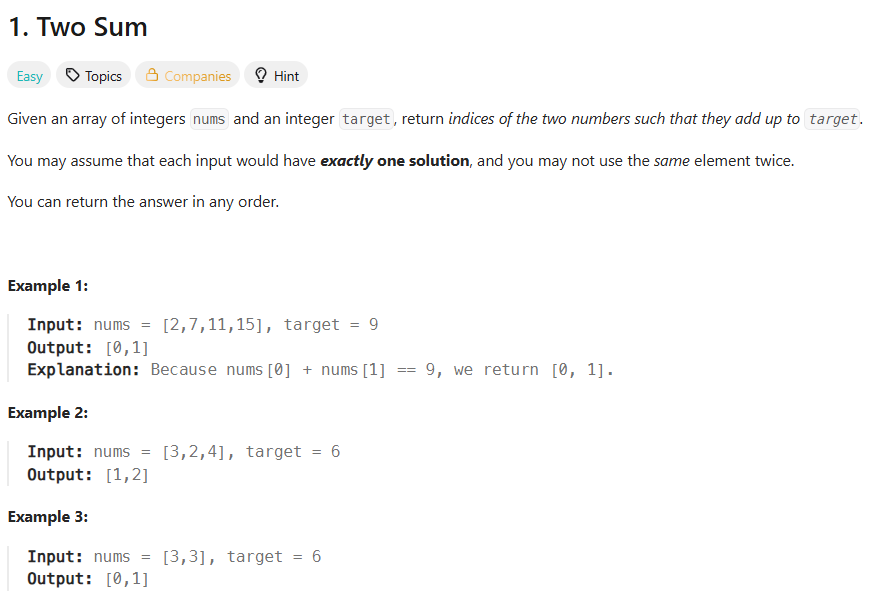
Easy | Leetcode 1. Two Sum

Question

給你一個整數陣列 nums 和一個整數 target，請你找出陣列中兩個數字，使它們的和等於 target，並回傳這兩個數字的索引。 假設每種輸入只會對應一個答案，而且同一個元素不能重複使用。

---

Solution

Solution1: Brute Force

解題概念：

使用兩層 for 迴圈，把所有可能的兩個元素加起來一一嘗試是否等於 target。

程式碼：

public class Solution1 {
    public static int[] twoSum(int[] nums, int target) {
        // 外層迴圈：從第0個元素開始
        for (int i = 0; i < nums.length; i++) {
            // 內層迴圈：從第 i+1 個開始，避免重複與自己相加
            for (int j = i + 1; j < nums.length; j++) {
                // 檢查兩數之和是否等於目標值
                if (nums[i] + nums[j] == target) {
                    return new int[] {i, j};
                }
            }
        }

        return new int[]{};
    }
}

複雜度分析：

• Time complexity: $O(n^2)$
  • 外層跑 n 次，內層平均跑 (n-1)/2 次，所以是平方級時間。
• Space complexity: $O(n + m)$
  • 沒有使用額外資料結構（只回傳答案），空間複雜度為常數等級。
    
    

Solution2: Sorting

解題概念：

1. 把 nums 轉成一個 2D 陣列 A，每個元素為 [值, 原本的 index]。
2. 接著排序這個 A，根據 值 來排。
3. 用雙指針：j 指向最小值、k 指向最大值，檢查兩數和是否為 target。
4. 若和太小，左邊往右；若和太大，右邊往左；接著重複檢查。
   
   

程式碼：

public class Solution2 {
    public static int[] twoSum(int[] nums, int target) {
        // 將 nums 陣列轉換為二維陣列
        int[][] A = new int[nums.length][2];

        for (int i = 0; i < nums.length; i++) {
            A[i][0] = nums[i]; // 元素0: 數值
            A[i][1] = i; // 元素1: 索引
        }

        // 根據值進行排序
        Arrays.sort(A, Comparator.comparingInt(a -> a[0]));

        // 利用雙指針，最左到最右加起來檢查是否 = target
        int j = 0, k = nums.length - 1;

        while(j < k) {
            int sum = A[j][0] + A[k][0];

            if (sum == target) {
                // 回傳原本的索引：記得小的放前，大的放後!!
                return new int[]{Math.min(A[j][1], A[k][1]), 
                                 Math.max(A[j][1], A[k][1])};
            }
            else if (sum < target) {
                // 總和過小，左指針向右（讓總和變大）
                j++;
            }
            else {
                // 總和過大，右指針向左（讓總和變小）
                k--;
            }
        }

        return new int[]{};
    }
}

複雜度分析：

• Time complexity: $O(log n)$
  • 建立 2D 陣列：$O(n)$
  • 排序：$O(n log n)$
  • 雙指針搜尋：$O(n)$
• Space complexity: $O(n)$
  • 額外使用一個 int[n][2] 來記錄數值和索引 → $O(n)$。
    
    

Solution3: HashMap (Two pass)

解題概念：

1. 我們使用一個 Map<Integer, Integer>（值 → 索引）來記錄每個數字出現的位置。
2. 對於每個數字 nums[j]，我們都想找出「另一個數 diff = target - nums[j]」是否已經出現過。
3. 如果存在這個數，且它的 index 不等於 j（不能自己加自己=target），那就是答案。
   
   

程式碼：

public class Solution3 {
    public static int[] twoSum(int[] nums, int target) {
        // 建立 Map：儲存每個數值對應的索引
        Map<Integer, Integer> map = new HashMap<>();

        // 先把所有數值及其索引放進 map 中
        for (int i = 0; i < nums.length; i++) {
            map.put(nums[i], i);
        }

        // 再次遍歷陣列，尋找是否存在配對值
        for (int j = 0; j < nums.length; j++) {
            int diff = target - nums[j]; // 所需的配對數字
            
            // 檢查 map 中是否有這個數，且不是自己
            if (map.containsKey(diff) && map.get(diff) != j) {
                return new int[]{j, map.get(diff)};
            }
        }

        return new int[]{};
    }
}

複雜度分析：

• Time complexity: $O(n)$
  • 第一次迴圈：把 nums 所有值加進 map → $O(n)$
  • 第二次迴圈：查找是否有符合的配對 → 每次查找 $O(1)$，總共 $O(n)$
• Space complexity: $O(n)$
  • map 需要存放最多 n 個 key-value pair（數值與其 index）。
    
    

Solution4: HashMap (One pass)

解題概念：

這個解法將「查找」與「記錄」結合在同一個迴圈中完成：

1. 對每個數 nums[i]，我們計算與它搭配會變成 target 的數字 diff = target - nums[i]。
2. 我們在遍歷時就「邊走邊查」，看 diff 是否已經存在於 HashMap 中。
   1. 如果有，那就表示我們之前遇過的某個數字可以和現在的 nums[i] 配對起來等於 target。
   2. 如果沒有，就把現在這個數字和索引記錄起來（以備之後使用）。
      
      

程式碼：

public class Solution4 {
    public static int[] twoSum(int[] nums, int target) {
        // 建立 Map：儲存每個數值對應的索引
        Map<Integer, Integer> prev_map = new HashMap<>();

        // 一次迴圈就完成：查找 + 記錄
        for (int i = 0; i < nums.length; i++) {
            int diff = target - nums[i];

            // 如果 map 中已經有這個補數，表示找到一組解
            if (prev_map.containsKey(diff)) {
                return new int[]{prev_map.get(diff), i};
            }
            
            // 如果沒有，就記錄目前這個數和它的 index
            prev_map.put(nums[i], i);
        }

        return new int[]{};
    }
}

複雜度分析：

• Time complexity: $O(n)$
  • 只走一次迴圈，每次都做一次查詢與插入（HashMap 這兩項都是 $O(1)$）。
• Space complexity: $O(n)$
  • 最壞情況下 HashMap 要存放 n 個元素（每個數字與其索引）。